• Variável aleatória
• Distribuição de probabilidade
• Distribuições discretas e contínuas
• Parâmetros da distribuição
• Esperança e variância
• Variáveis aleatórias discretas mais usadas em ecologia

Qual a probabilidade de que nasça apenas um macho em uma ninhada de cinco filhotes de cachorro-do-mato, se a definição do sexo é independente para cada um, e as chances de nascerem machos e fêmeas são iguais?

Essa probabilidade é obtida pela distribuição binomial, com o seguinte comando no R:

> dbinom(x=1,size=5,prob=0.5)

Esta função retorna a probabilidade do número de sucessos de um total de tentativas independentes, dada a probabilidade de sucesso em cada tentativa. O número de tentativas (size) e a probabilidade (prob) são os parâmetros da função.

Qual sua expectativa se alterarmos os parâmetros? Por exemplo, experimente reduzir as chances de nascimento de machos para um terço:

> dbinom(x=1,size=5,prob=1/3)

E se aumentarmos o tamanho da ninhada?

> dbinom(x=1,size=10,prob=0.5)

Antes de prosseguir, certifique-se que você compreendeu os motivos das diferenças dos três resultados.

Voltando ao primeiro caso de variável binomial, os resultados possíveis para uma ninhada são 0, 1, 2, 3, 4 ou 5 machos. Suas probabilidades são:

> p1<- dbinom(x=0:5, size=5, prob=0.5)
> names(p1) <- 0:5
> p1

O que podemos colocar em um gráfico:

> plot(0:5,p1,type="h",lwd=5,col="blue",xlab="N de machos",ylab="Probabilidade")

Todos os valores entre zero e cinco machos podem ocorrer, mas alguns são mais prováveis. Se tivéssemos uma amostra de muitas ninhadas, qual seria o número médio de machos? Podemos simular essa situação, sorteando mil valores de uma distribuição binomial, com os mesmos parâmetros:

> sim1 <- rbinom(n=1000,size=5,prob=0.5)

Os primeiros valores são:

> head(sim1)

E a média dos mil valores é obtida com:

> mean(sim1)

Este número faz sentido para você? Ele é uma aproximação da esperança da variável aleatória.

O valor teórico da esperança estatística de uma variável aleatória discreta é obtido multiplicando-se cada valor por sua probabilidade, e então somando-se estes resultados¹⁾:

$$E[X] = \sum_{i=1}^n x_i P(X=x_i)$$

No R podemos calcular isto com os comandos:

> esper <- sum(0:5*p1)
> esper

Marque este valor no eixo x do gráfico:

> mtext(at=esper,text="^",side=1,line=0.5,cex=2,col="red")

Uma interpertação da esperança é que ela é o centro de massa de uma distribuição de probabilidades. Se o eixo do gráfico fosse uma balança, a média seria o ponto de apoio para que os dois lados se equilibrassem. A esperança é a média da distribuição, o valor médio esperado para a variável aleatória.

Calcule as probabilidades para ninhadas de 5 e 10 filhotes, com probabilidades de 1/3 e 0,5 de nascimento de machos:

> p2 <- dbinom(0:5,size=5,prob=1/3)
> p3 <- dbinom(0:10,size=10,prob=0.5)
> p4 <- dbinom(0:10,size=10,prob=1/3)

Faça gráficos das distribuições de probabilidade para avaliar o efeito das mudanças dos parâmetros:

> maxp <- max(c(p1,p2,p3,p4))
> par(mfrow=c(2,2))
> plot(0:5,p1,main="n=5, p=0.5",  xlim=c(0,10), ylim=c(0,maxp),type="h",lwd=5,xlab="N de machos",ylab="Probabilidade")
> plot(0:5,p2,main="n=5, p=1/3",  xlim=c(0,10),ylim=c(0,maxp),type="h",lwd=5,xlab="N de machos",ylab="Probabilidade")
> plot(0:10,p3,main="n=10, p=0.5",xlim=c(0,10),ylim=c(0,maxp),type="h",lwd=5,xlab="N de machos",ylab="Probabilidade")
> plot(0:10,p4,main="n=10, p=1/3",xlim=c(0,10),ylim=c(0,maxp),type="h",lwd=5,xlab="N de machos",ylab="Probabilidade")
> par(mfrow=c(1,1))

Uma variável Poisson é um modelo do número de eventos em uma unidade de tempo ou espaço, dado que a taxa de eventos por unidade é constante, e os eventos são independentes. O único parâmetro da Poisson é $$\lambda$$, a taxa de eventos por unidade.

Portanto, se um certo número de objetos está distribuído ao acaso por uma área, e esta área é dividida em quadrículas de mesmo tamanho, o número de objetos por quadrículas pode ser descrito como uma variável Poisson. Neste caso, o parâmetro $$\lambda$$ será o total de objetos dividido pelo total de quadrículas.

Para simular uma situação como esta, vamos distribuir ao acaso 1.000 plantas em uma área de 20 x 20 metros, divida em quadrículas de 1 x 1 m, como na figura abaixo

Primeiro geramos mil coordenadas $$x$$ e $$y$$ entre 0 e 20, de uma distribuição uniforme²⁾:

set.seed(42) ## fixa a semente de números aleatórios
x <- runif(n=1000,min=0, max=20)
y <- runif(n=1000,min=0, max=20)

Para simular as quadrículas, dividimos as coordenadas em fatores com intervalo de um, que representam segmentos de um metro. As linhas recebem rótulos de 1 a 20, e as colunas rótulos de A a T:

x.parc <- cut(x,breaks=0:20, labels=1:20)
y.parc <- cut(y,breaks=0:20, labels=LETTERS[1:20])

E então usamos a função table para contar quantos valores há em cada combinação destes fatores. Esta tabela cruzada é então transformada em um data frame e o resultado atribuído a um objeto:

cont <- data.frame(table(x.parc,y.parc))

O objeto resultante terá a contagem de pontos em cada combinação dos rótulos de linhas e colunas, ou seja, quantos plantas há em cada quadrícula.:

> head(cont)
  x.parc y.parc Freq
1      1      A    1
2      2      A    1
3      3      A    3
4      4      A    3
5      5      A    1
6      6      A    3
> tail(cont)
    x.parc y.parc Freq
395     15      T    1
396     16      T    2
397     17      T    3
398     18      T    1
399     19      T    2
400     20      T    2

Contamos o número de parcelas com cada abundância com a função table

   freq.ab <- table(cont$Freq)

Dividimos estas contagens pelo total de parcelas para obter proporções, e as representamos em um gráfico aplicando a função plot:

plot(freq.ab/400, xlab="N de indivíduos na parcela", 
     ylab="Proporção das parcelas")

Em seguida adicionamos as probabilidades previstas para uma variável Poisson com a mesma taxa de ocorrência, que é de 1.000 plantas em 400 parcelas ($$\lambda = 0,25$$):

points(x=0:max(cont$Freq), y=dpois(0:max(cont$Freq), 
       lambda=1000/400), type="b", 
       col="blue", lty=2)

Avalie visualmente a concordância entre os valores previstos e simulados.

Caso queira reproduzir a primeira figura deste tutorial, os comandos são:

plot(x=x,y=y,axes=F, xlab="", ylab="", 
     xlim=c(-1,20),ylim=c(0,21))
segments(x0=rep(0,20),y0=0:20,
         x1=rep(20,20),y1=0:20, col="gray", lty=2)
segments(x0=0:20,y0=rep(0,20),
         x1=0:20,y1=rep(20,20),col="gray", lty=2)
text(y=seq(0.5,19.5,by=1),x=-1, labels=20:1)
text(x=seq(0.5,19.5,by=1),y=21, labels=LETTERS[1:20])

Uma variável geométrica é um modelo para o número de tentativas negativas até que se obtenha o primeiro resultado positivo, com uma probabilidade constante de ter um resultado positivo em cada tentativa.

Formalmente, é o número de fracassos até o primeiro sucesso em uma sequência de experimentos de Bernoulli.

Um exemplo biológico seria a sobrevivência de indivíduos em intervalos discretos de tempo, com uma taxa de mortalidade constante. A cada intervalo discreto de tempo, cada indivíduo da população tem a probabilidade $$p$$ de morrer, portanto a probabilidade de que a morte ocorra após $$x$$ intervalos será:

$$P(x) = p(1-p)^x$$

Que é a distribuição de probabilidades da variável aleatória geométrica.

Com o R podemos simular, para um indivíduo, uma sequência de intervalos, sendo que em cada intervalo sorteamos se o indivíduo morrerá ou não, com uma probabilidade fixa. Usamos a função sample para sortear entre ““vivo”” e “morto” com probabilidades $$1-p$$ e $$p$$, a cada intervalo. Usamos a função while para manter o sorteio correndo até a morte do indivíduo (primeiro sorteio do valor “morto”), e contamos quantos sorteios ocorreram até que isto aconteça:

> p.morte <- 0.2
> result <- 0 
> while(sample(c("vivo","morto"),prob=c(1-p.morte,p.morte),size=1)=="vivo"){
      result <- result+1
    }
> result
[1] 8

Agora vamos criar uma função que repete esta simulação para vários indivíduos. Seus argumentos são o número de indivíduos (N) e a probabilidade de morrer a cada intervalo (p.morte):

sobrevive <- function(N=1000, p.morte=0.2){
  result <- rep(0,N)
  for(i in 1:N){
    while(
          sample( c("vivo","morto"), 
                 prob= c(1-p.morte,p.morte),size=1)=="vivo"){
      result[i] <- result[i]+1
    }
  }
  result
}

E podemos fazer uma simulação para 2.000 indivíduos, com probabilidade de morte de 0,2:

sim2 <- sobrevive(N=2000)

E agora vamos fazer um gráfico do número de indivíduos que viveram até cada valor de intervalo. Para isto, primeiro criamos uma variável de fator com valores observados de intervalo, mas com níveis de zero ao valor máximo, para garantir que mesmo valores sem observações na amostra sejam representados:

 sim2.f <- factor(sim2,levels=0:max(sim2))

E então aplicamos a função plot sobre a tabulação desta variável, divida pelo total de indivíduos para ser uma proporção:

plot(table(sim2.f)/length(sim2), xlab="Tempo de vida",
      ylab="Proporção dos Indivíduos")      

Por fim acrescentamos os valores de probabilidade da variável geométrica:

 points(0:max(sim2),dgeom(0:max(sim2),prob=0.2),type="b",col="blue")

Avalie a correspondência entre os valores simulados das proporções de indivíduos e as probabilidades teóricas.

A variável binomial negativa é uma extensão da variável geométrica, que descreve a probabilidade de fracassos em uma sequência de experimentos de Bernoulli até que se obtenha $$n$$ sucessos, dado que a probabilidade $$p$$ de sucesso a cada tentativa é constante.

Esta variável pode ser reparametrizada , substituindo-se o $$p$$ por um parâmetro $$\mu$$, que corresponde à esperança da distribuição, ou seja, sua média.

$$\mu=\frac{n(1-p)}{p}$$

Nesta formulação, $$n$$ pode ter qualquer valor e pode ser interpretado como um índice de dispersão, e recebe a nome de $$k$$, para distinguí-lo da outra parametrização. Quanto menor o $$k$$, maior a concentração da massa da distribuição nos valores baixos, o que dá à distribuição uma forte assimetria à direita.

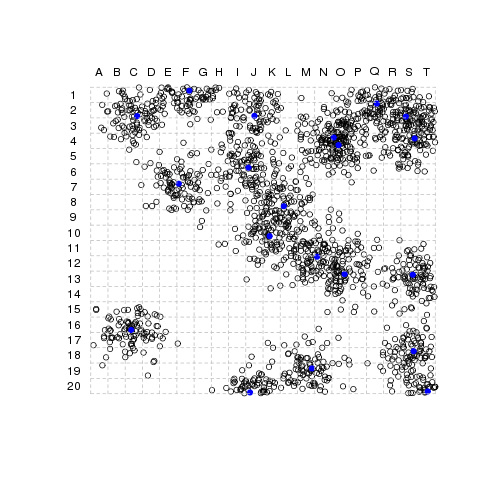
Por esta propriedade, a binomial negativa é um modelo simples para descrever contagens de eventos agregados por unidade amostral. Neste tutorial seguiremos a mesma lógica do tutorial sobre o processo Poisson, mas agora simulando uma planta distribuída em agregados em uma área de 20 x 20 m, como na figura abaixo.

Para simular este padrão, primeiro sorteamos 20 coordenadas entre 0 e 20 m de uma distribuição uniforme. Estes 20 pontos distribuídos ao acaso serão os centros dos agregados, representados em azul na figura.

set.seed(42)
cx <- runif(20,0,20)
cy <- runif(20,0,20)

Em seguida sorteamos 2.000 coordenadas de uma distribuição normal padronizada ³⁾, e somamos a cada uma destas coordenadas as coordenadas dos centros. Com isto teremos 100 pontos agregados em torno de cada centro ⁴⁾.

px <- rnorm(2000)
py <- rnorm(2000)
x1 <- cx+px
y1 <- cy+py

Em seguida usamos a indexação para ficar apenas com os pontos que estão dentro da área (com coordenadas entre 0 e 20):

x2 <- x1[x1>0&x1<20&y1>0&y1<20]
y2 <- y1[x1>0&x1<20&y1>0&y1<20]

Para simular as quadrículas, dividimos as coordenadas em fatores com intervalo de um, que representam segmentos de um metro. As linhas recebem rótulos de 1 a 20, e as colunas rótulos de A a T:

x2.parc <- cut(x2,breaks=0:20, labels=1:20)
y2.parc <- cut(y2,breaks=0:20, labels=LETTERS[1:20])

E então usamos a função table para contar quantos valores há em cada combinação destes fatores. Esta tabela cruzada é então transformada em um data frame e o resultado atribuído a um objeto:

 cont2 <- data.frame(table(x2.parc,y2.parc))

O número de indivíduos de cada parcela, que é a coluna Freq deste objeto, é transformado em um fator, que tem níveis de zero ao máximo de indivíduos observado em uma parcela:

  cont2.f <- factor(cont2$Freq, levels=0:max(cont2$Freq))

Dividimos estas contagens pelo total de parcelas para obter proporções, e as representamos em um gráfico aplicando a função plot:

plot(table(cont2.f)/400, xlab="N de indivíduos na parcela",
     ylab="Proporção das parcelas")

Em seguida adicionamos as probabilidades previstas para uma variável Poisson com a mesma taxa de ocorrência, que é o total de plantas dividido por 400 parcelas:

points(x=0:max(cont2$Freq),y=dpois(0:max(cont2$Freq),
       lambda=sum(cont2$Freq)/400), 
       type="b", col="blue", lty=2)

A variável Poisson não é um bom modelo, o que era esperado, já que ela descreve eventos independentes, isto é, distribuídos aleatoriamente.

Vamos então comparar o desempenho da Poisson com o da Binomial Negativa. Sabemos que um dos parâmetros desta distribuição, $$\mu$$, corresponde à taxa de ocorrência, mas precisamos estimar o outro, que é o índice de dispersão $$k$$. Para isto usaremos a função fitdistr do pacote MASS. Aplicada a um vetor numérico, esta função retorna a estimativa dos parâmetros⁵⁾, que podem ser extraídos com a função coef:

require(MASS) # basta uma vez por seção
cont2.nb <- coef(fitdistr(cont2$Freq,"negative binomial"))
cont2.nb

Com os valores estimados dos parâmetros podemos acrescentar ao gráfico as probabilidades previstas pela Binomial Negativa para cada abundância:

points(x=0:max(cont2$Freq),y=dnbinom(0:max(cont2$Freq),
       mu=cont2.nb[2],size=cont2.nb[1]), 
       type="b", col="red", lty=2)

Note como a probabilidade de valores pequenos é maior na Binomial Negativa, em comparação com a Poisson, embora ambas tenham a mesma taxa de ocorrência. É isto que você esperaria no caso de agregação espacial?

O próximo tutorial mostra como a Binomial Negativa se aproxima de uma Poisson se aumentamos o valor do parâmetro $$k$$.

Caso queira reproduzir a figura do padrão espacial, os comandos são:

plot(x=x2,y=y2,axes=F, xlab="", ylab="", xlim=c(-1,20),ylim=c(0,21))
points(cx,cy, col="blue", pch=19)
segments(x0=rep(0,20),y0=0:20,x1=rep(20,20),y1=0:20, col="gray", lty=2)
segments(x0=0:20,y0=rep(0,20),x1=0:20,y1=rep(20,20),col="gray", lty=2)
text(y=seq(0.5,19.5,by=1),x=-1, labels=20:1)
text(x=seq(0.5,19.5,by=1),y=21, labels=LETTERS[1:20])
x2.parc <- cut(x2,breaks=0:20, labels=1:20)
y2.parc <- cut(y2,breaks=0:20, labels=LETTERS[1:20])

Use os comandos abaixo para plotar gráficos das distribuições de probabilidade de uma Variável Poisson com média 4 e variáveis Binomiais de mesma média e parâmetro de dispersão crescentes. Quais suas conclusões?

par(mfrow=c(2,2))
plot(0:30, dpois(0:30,lambda=4),type="b", xlab="x", ylab="p",
     ylim=c(0,0.35),
     main=expression(paste("Poisson, ", lambda,"=4")))
plot(0:30, dnbinom(0:30,mu=4,size=0.5),type="b",
     ylim=c(0,0.35), xlab="x", ylab="p",
     main=expression(paste("Bin. Neg., ", mu,"=4", ", k=0.5")))
plot(0:30, dnbinom(0:30,mu=4,size=1.5),type="b",
     ylim=c(0,0.35), xlab="x", ylab="p",
     main=expression(paste("Bin. Neg., ", mu,"=4", ", k=1.5")))
plot(0:30, dnbinom(0:30,mu=4,size=20),type="b",
     ylim=c(0,0.35), xlab="x", ylab="p",
     main=expression(paste("Bin. Neg., ", mu,"=4", ", k=20")))
par(mfrow=c(1,1))

Compare a distribuição de probabilidades da variável aleatória Geométrica com parâmetro $$p$$ (probabilidade de sucesso em cada tentativa) igual a 0,2 e a de uma variável Binomial Negativa com o mesmo valor de $$p$$, e parâmetro $$n$$ (número de sucessos desejados) igual a um.

par(mfrow=c(1,2))
plot(0:30,dgeom(0:30,prob=0.2),xlab="N de fracassos", ylab="P",
     main="Geométrica, p=0,2")
plot(0:30, dnbinom(0:30,size=1,prob=0.2),xlab="N de fracassos", ylab="P",
     main="Bin. Neg., n=1, p=0,2")
par(mfrow=c(1,1))

Como você explica este resultado?

Compare a distribuição de probabilidades de uma variável Binomial com parâmetro $$n$$ alto e parâmetro $$p$$ baixo com uma Poisson de mesma média ⁶⁾:

par(mfrow=c(1,2))
plot(0:10, dbinom(0:10, prob=0.01, size=200), xlab="x", ylab="P",
     main="Binomial, n=200, p=0,01")
plot(0:10, dpois(0:10,lambda=0.01*200), xlab="x", ylab="P",
     main=expression(paste("Poisson, ", lambda,"=2")))
par(mfrow=c(1,1))

1. Quais suas conclusões?
2. Há uma interpretação biológica para isto?

• Introdução à Modelagem Estatística
• Variáveis Aleatórias Discretas

• Portal sobre distribuições de probabilidades na Wikipedia: http://en.wikipedia.org/wiki/Probability_distribution

• Distribuições interativas on-line do Statistics Online Computational Resource da UCLA: http://www.socr.ucla.edu/htmls/SOCR_Distributions.html

• Capítulo sobre variáveis aleatórias do e-book de Probabilidade e Estatística da UCLA: http://wiki.stat.ucla.edu/socr/index.php/EBook#Chapter_IV:_Probability_Distributions

• Mapa interativo de relações entre as distribuições de probabilidades. Um resumo em html do execelente mapa de Leemis & McQueston (2008).

• Um excelente resumo das propriedades e relações entre distribuições de probabilidade:
  • Leemis, L. M., and J. T. McQueston. 2008. Univariate Distribution Relationships. The American Statistician 62:45-53.pdf na página do autor

• Tópico sobre distribuições estatísticas no R na apostila on-line do curso Uso da Linguagem R para Análise de dados Ecológicos.

• BINOMIAL
  • Parâmetros: $$p$$ , $$n$$
  • Parâmetros no R: prob, size
  • Função no R: [dpqr]binom
  • Suporte: $$0, n$$
  • Assimetria: direita, esquerda, nenhuma
  • Esperança: $$np$$
  • Variância: $$np(1-p)$$

• BINOMIAL NEGATIVA
  • Parâmetros: $$p,n$$ OU $$\mu,k$$
  • Parâmetros no R: prob, size OU mu, size
  • Função no R: [dpqr]nbinom
  • Suporte: $$0, \infty$$
  • Assimetria: direita
  • Esperança: $$\mu=\frac{n(1-p)}{p}$$
  • Variância: $$\mu+ \frac{\mu^2}{k}=\frac{n(1-p)}{p^2}$$

• GEOMÉTRICA
  • Parâmetro: $$p$$
  • Parâmetro no R: prob
  • Função no R: [dpqr]geom
  • Suporte: $$0, \infty$$
  • Assimetria: direita
  • Esperança: $$\frac{1-p}{p}$$
  • Variância: $$\frac{1-p}{p^2}$$

• POISSON
  • Parâmetro: $$\lambda$$
  • Parâmetro no R: lambda
  • Função no R: [dpqr]pois
  • Suporte: $$0, \infty$$
  • Assimetria: direita a não
  • Esperança: $$\lambda$$
  • Variância: $$\lambda$$

Indique os tutoriais e partes da leitura básica que merecem mais atenção na discussão aqui.