Tabela de conteúdos
2. Variáveis Aleatórias Contínuas
Conceitos
- Função de densidade probabilística
- Função de probabilidade acumulada
- Esperança e variância de variáveis contínuas
- Teorema Central do Limite
- Variáveis aleatórias contínuas mais usadas em ecologia
Tutoriais
Função de Densidade e Probabilidade
É importante ter clara a diferença entre a função de densidade de probabilidade de uma variável aleatória contínua e a probabilidade desta variável assumir um valor dentro de um intervalo.
A primeira não é uma probabilidade, e pode ter valores maiores do que um. No caso de uma variável normal, isto acontece quando média e desvio-padrão são baixos.
A função dnorm no R retorna o valor da função de densidade da normal para um dado valor da variável aleatória. Para uma normal com parâmetros $$\mu=2$$ e $$\sigma=0,1$$ os valores da função de densidade para $$\mu \+- 1,5\sigma$$ são:
> dnorm(2+c(-0.15,0.15),mean=2,sd=0.1) [1] 1.295176 1.295176
Aplicando a função curve à função dnorm podemos traçar o gráfico da função dentro de um intervalo dado pelos argumentos from e to. Vamos fazer isto para a variável normal definida acima, no intervalo $$\mu \+- 3\sigma$$
curve(dnorm(x,mean=2,sd=0.1),from=1.7, to=2.3,
xlab="x",ylab="densidade de probabilidade")
Vamos acrescentar neste gráfico os valores que calculamos acima:
points(2+c(-0.15,0.15),dnorm(2+c(-0.15,0.15),mean=2,sd=0.1),
col="red", pch=19, cex=1.5)
segments(x0=c(2+c(-0.15,0.15,0.15)),
y0=c(0,0,dnorm(2.15,mean=2,sd=0.1)),
x1=c(2+c(-0.15,0.15),1.5),
y1=dnorm(2+c(-0.15,0.15,0.15),mean=2,sd=0.1),
col="red", lty=2)
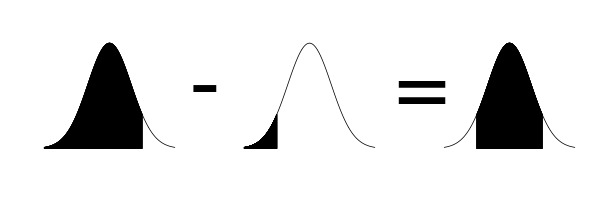
Para uma variável aleatória a probabilidade só pode ser definida para um intervalo, e corresponde à área sob a curva que está dentro delimitada por este intervalo. Vamos criar uma função no R para preencher esta área no gráfico da curva normal 1):
area.norm <- function(from,to,mean,sd,cor="red",shade=50,...){
len <- (to-from)*shade
x <- seq(from,to,length=len)
segments(x0=x,x1=x,y0=rep(0,len),y1=dnorm(x,mean=mean,sd=sd),col=cor)
}
E agora aplicá-la para colorir de vermelho a área delimitada por $$\mu \+- 1,5\sigma$$ no gráfico que criamos:
area.norm(1.85,2.15,mean=2,sd=0.1)
A área sob uma função é sua integral. Podemos calculá-la com a função de integração do R 2):
integrate(dnorm,lower=1.85, upper=2.15,mean=2,sd=0.1)
A integral de qualquer função de densidade probabilística no intervalo que contém todos os valores da variável aleatória é um. Verifique isto para a normal, integrando-a de $$-\infty$$ a $$\infty$$:
integrate(dnorm,lower=-Inf, upper=Inf,mean=2,sd=0.1) integrate(dnorm,lower=Inf, upper=Inf) ## normal padronizada
A integral do limite inferior da variável aleatória até um certo valor é a função de densidade acumulada. Para a normal, a função no R é pnorm. A área entre dois valores pode ser obtida subtraindo-se suas probabilidades acumuladas:
O que você obtém com o comando:
pnorm(2.15,mean=2,sd=0.1)-pnorm(1.85,mean=2,sd=0.1)
A função pnorm tem o argumento lower.tail, que permite calcular a probabilidade a partir de um ponto, isto é, da cauda posterior ao valor da variável aleatória (lower.tail=FALSE). Com isto, outra maneira de obter a probabilidade para o mesmo intervalo é:
1-(pnorm(2.15,mean=2,sd=0.1,lower.tail=F)+pnorm(1.85,mean=2,sd=0.1))
Por fim, como o intervalo é simétrico em torno da média, e a curva normal também o é, uma terceira maneira de fazer o cálculo é:
1-2*pnorm(1.85,mean=2,sd=0.1,lower.tail=F)
Extras
Se quiser reproduzir a figura deste tutorial, o código em R é
png("dif_normal.png",height=200,width=600)
par(mfrow=c(1,3))
curve(dnorm(x,mean=2,sd=0.1),from=1.7, to=2.3,
xlab="",ylab="",axes="F")
area.norm(1.7,2.15,mean=2,sd=0.1,cor="black")
curve(dnorm(x,mean=2,sd=0.1),from=1.7, to=2.3,
xlab="",ylab="",axes="F")
area.norm(1.7,1.85,mean=2,sd=0.1,cor="black")
curve(dnorm(x,mean=2,sd=0.1),from=1.7, to=2.3,
xlab="",ylab="",axes="F")
area.norm(1.85,2.15,mean=2,sd=0.1,cor="black")
mtext(c("-","="),at=c(0.6,1.6),padj=1.1,cex=8)
dev.off()
Esperança de uma Variável Contínua
A esperança de uma variável aleatória contínua é
$$E[X]\ = \ \int x cdot f(x) \ dx$$
Onde $$f(x)$$ é a função de densidade probabilística.
Vamos verificar isto numericamente para a variável exponencial, cuja média é o inverso de seu único parâmetro, $$\lambda$$. Começamos definindo uma função no R que é o produto da densidade pelo valor da variável aleatória:
esper.exp <- function(x,taxa){
dexp(x,rate=taxa)*x
}
Agora usamos a função integrate para fazer a integração numérica desta função no suporte da exponencial ($$0$$ a $$\infty$$), para uma variável exponencial com $$\lambda=0.1$$:
integrate(esper.exp,0,Inf,taxa=1/10)
Compare o valor obtido com o valor teórico da esperança.
Histograma de Densidade
Para comparar a distribuição de dados com alguma variável aleatória, podemos usar um histograma re-escalonado para densidade.
Para exemplificar, usaremos os perímetros à altura do peito de fustes de caixeta amostradas em um inventário florestal.
Primeiro criamos um objeto com os dados de interesse, que são os fustes da caixeta em Chauás:
caixeta <- read.csv("caixeta.csv")
chauas <- caixeta[caixeta$local=="chauas"
&caixeta$especie=="Tabebuia cassinoides",]
E então criamos um fator para as classes de CAP, com intervalos de 100 mm:
chauas$cap.class <- cut(chauas$cap,breaks=seq(100,800,by=100))
Um gráfico da tabulação deste fator é um histograma de frequências:
barplot(table(chauas$cap.class),space=0)
Dividindo-se os valores pelo total de fustes temos um histograma de frequências relativas:
barplot(table(chauas$cap.class)/length(chauas$cap.class))
Finalmente, dividindo novamente estes valores pelas amplitude do intervalo de classe usado (100 mm) temos um histograma de densidade:
barplot(table(chauas$cap.class)/(length(chauas$cap.class)*100),
space=0)
Neste histograma, a soma das áreas das barras é um. A função hist tem um argumento prob que converte a escala para densidade:
hist(chauas$cap,breaks=8,prob=T,
xlab="CAP (cm)",ylab="Densidade")
Nesta escala podemo sobrepor a funções de densidade, como a normal:
curve(dnorm(x,mean=mean(chauas$cap),
sd=sd(chauas$cap)),add=T,col="blue")
A variável normal
As companhias aéreas norte-americanas garantem que 98% de seus passageiros não terão problemas para se acomodar nos assentos da classe econômica. Para isso, usam um modelo que descreve a distribuição das larguras dos quadris dos homens norte-americanos como uma variável normal, com média de 14,4 polegadas, e desvio-padrão de 1,0 polegada.
Faça um gráfico desta distribuição de probabilidades:
curve(dnorm(x,mean=14.4,sd=1),from=8, to=20,
xlab="Largura (in)",ylab="densidade de probabilidade")
Para definir a largura do assento, é preciso saber o limite superior do intervalo que contêm 98% da população. Esse é o quantil de 98% da distribuição, no caso uma normal com média de 14,4 e desvio-padrão de 1,0 polegadas.
Calcule o valor deste quantil com o comando:
larg <- qnorm(mean=14.4,sd=1,p=0.98) larg
Este é o valor que delimita 98% da área sob a curva normal. Usando a função criada no tutorial anterior podemos visualizar no gráfico a área que vai até o quantil calculado acima:
area.norm(8,larg,mean=14.4,sd=1)
Variando os Parâmetros da Normal
Imagine que o desvio-padrão para o exemplo dos quadris norte-americanos seja 50% maior. O que deve ocorrer com o quantil de 98%? Verifique sua expectativa com o comando:
qnorm(mean=14.4,sd=1.5,p=0.98)
Repita o gráfico do tutorial anterior, e adicione ao gráfico a distribuição de probabilidades com o novo valor do parâmetro desvio-padrão:
curve(dnorm(x,mean=14.4,sd=1),from=8, to=20,
xlab="Largura (in)",ylab="densidade de probabilidade")
curve(dnorm(x,mean=14.4,sd=1.5), add=T, col="blue")
Os parâmetros da distribuição normal correspondem à média e ao desvio-padrão. Explore o comportamento da curva com a mudança de seus parâmetros:
cores <- rainbow(n=4)
curve(dnorm(x),from=-8,to=8, col=cores[1])
curve(dnorm(x,sd=2), col=cores[2], add=T)
curve(dnorm(x,mean=2), col=cores[3], add=T)
curve(dnorm(x,mean=2,sd=2), col=cores[4], add=T)
legend(-7.5,0.3,legend=c("média=0,sd=1","média=0,sd=2",
"média=2,sd=1","média=2,sd=2"),lty=1,col=cores)
Teorema Central do Limite
O Teorema Central do Limite (TCL) prova que as médias de amostras independentes tomadas de uma mesma distribuição convergem para uma distribuição normal. A média desta normal é a mesma da distribuição de onde vieram as amostras, e a variância é igual à variância da distribuição original, dividida pelo tamanho das amostras.
Verifique isto com o seguinte tutorial:
Sorteie dez mil números de uma distribuição muito diferente de uma normal, como uma Poisson com média baixa:
vals <- rpois(10000,lambda=0.5))
Agora imagine que estes valores foram obtidos de mil amostras independentes, cada uma de tamanho dez. Vamos criar um fator que rotule as amostras de um a mil:
cod.amostras <- factor(rep(1:1000,each=10))
Agora podemos calcular a média de cada uma dessas amostras:
medias.vals <- tapply(vals,cod.amostras,mean)
E fazer um histograma dessas mil médias:
hist(medias.vals,prob=T)
E sobrepor a função de densidade da normal, com os parâmetros previstos pelo TCL:
curve(dnorm(x,mean=0.5,sd=sqrt(0.5/10)),add=T,col="blue")
Uma outra ótima maneira de avaliar a normalidade é com o gráfico de quantis normais:
qqnorm(medias.vals) qqline(medias.vals)
Repita os procedimentos, com mil amostras de tamanho 50. Quais suas conclusões?
Variável Bernoulli Tendendo à Normal?
Uma maneira simples de formular o Teorema Central do Limite é que a soma ou a média de muitas variáveis aleatórias tende a uma variável normal. Esta tendência é válida mesmo para variáveis com distribuições muito diferentes da normal e que não tenham os mesmos parâmetros.
Neste tutorial investigaremos se o TCL pode nos ajudar a propor um modelo para a riqueza de espécies em um conjunto de áreas. Vamos simular um cenário em que a ocorrência de cada espécie é uma variável Bernoulli ($$1$$ = presente, $$0$$ = ausente), cujo único parâmetro ($$p$$ a probabilidade de ocorrência) varia entre espécies.
Vamos assumir que as probabilidades de ocorrência também são variáveis aleatórias. Uma escolha natural é a variável Beta, que está restrita a valores entre zero e um.
Para simular uma metacomunidade com 300 espécies, sorteamos 300 valores da variável beta representada acima:
p.oc <- rbeta(300, shape1=1,shape2=5)
Em seguida criamos uma função que faz $$N$$ experimentos de Bernoulli, tomando um valor $$1$$ com probabilidade $$p$$ e valor $$0$$ com probabilidade $$1-p$$
ocorre <- function(p,N)sample(c(0,1),size=N,replace=T,prob=c(1-p,p))
Aplicando esta função às probabilidades de ocorrência sorteadas no passo anterior, obtemos uma matriz com $$100$$ linhas (locais) e $$300$$ colunas (espécies):
matriz <- sapply(p.oc,ocorre,N=100)
A soma das linhas são o número de espécies em cada um dos $$100$$ locais
riquezas <- apply(matriz,1,sum)
Cuja distribuição pode ser comparada com função de densidade de uma normal de mesma média e desvio-padrão:
hist(riquezas,prob=T,xlab="N de espécies",
ylab="Densidade de Probabilidade")
curve(dnorm(x,mean=mean(riquezas),sd=sd(riquezas)),
add=T,col="blue")
Avalie também o ajuste a uma normal com o gráfico de quantis teóricos:
qqnorm(riquezas) qqline(riquezas)
Extras
Se quiser repoduzir o gráfico da variável beta deste tutorial o comando é:
curve(dbeta(x,shape1=1,shape2=5),0,1,
xlab="x",ylab="Densidade de Probabilidade")
Variável Exponencial
A variável exponencial é a análoga contínua da variável geométrica. Ela foi criada para descrever o tempo de espera até a primeira ocorrência de um evento, dado que ele tem uma taxa de ocorrência $$\lambda$$ constante.
Vamos simular esta situação, imaginando que você acompanha um animal por até duas horas, sempre no mesmo horário. Sua variável de interesse é o tempo até que ele apresente um certo comportamento pela primeira vez. A taxa média com que este comportamento ocorre neste horário é de 0,05/minuto.
A distribuição desta variável aleatória pode ser simulada repetindo o estudo muitas vezes. A cada uma delas haverá um certo número de comportamentos, com uma média de $$0,05 \times 120 = 6$$ vezes. Supondo que estes eventos estão distribuídos aleatoriamente entre os dias, o número de eventos a cada dia será uma variável Poisson. Para simular 10.000 repetições, sorteamos esta quantidade de valores de uma Poisson com taxa de ocorrência por dia de 6:
n <- rpois(10000,6)
O total de eventos será então a soma destes valores sorteados. Em seguida sorteamos este número de valores de uma distribuição uniforme, com o mínimo de $$0$$ e máximo de $$120$$. Estes serão os horários de ocorrência de cada evento, em cada repetição do estudo.
vals <- runif(sum(n),0,120)
E criamos um fator para identificar cada repetição do estudo:
cod.amostras <- factor(rep(1:10000,n))
Com isto, podemos usar a função tapply para identificar o menor valor de cada repetição:
primeiro <- tapply(vals,cod.amostras,min)
E agora construímos um histograma de densidade desta variável, e sobrepomos a função de densidade da variável exponencial:
hist(primeiro,prob=T, xlab="Tempo de Espera (min)",
ylab="Densidade Probabilística")
curve(dexp(x,rate=6/120),add=T,col="blue")
Avalie visualmente a concordância com o modelo teórico.
Variável Gama
A variável Gama foi criada como uma extensão da exponencial, para descrever o tempo de espera até que um certo número de eventos ocorram, dada uma taxa constante de ocorrência. Devido à sua flexibilidade, posteriormente foi adotada como modelo heurístico para descrever variáveis com distribuições de probabilidade assimétricas.
Usando a simulação do tutorial anterior, podemos obter os tempos de espera até que o animal apresente o comportamento de interesse pela segunda vez. Para isto, criamos uma função que retorna o n-ésimo menor valor de um vetor de números
enesimo <- function(x,n)sort(x)[n]
E aplicamos esta função a cada repetição do estudo:
segundo <- tapply(vals,cod.amostras,enesimo,n=2)
Para então fazer um histograma de densidade com estes dados
hist(segundo,prob=T, xlab="Tempo de Espera (min)",
ylab="Densidade Probabilística")
Podemos então sobrepor a este histograma a curva da função de densidade probabilística da variável Gama, com os parâmetros teóricos de taxa de ocorrência (rate) e número de eventos a esperar (shape):
curve(dgamma(x,rate=6/120,shape=2),add=T,col="blue")
Variável Log-Normal
Assim como a variável normal descreve a soma ou média de muitas variáveis aleatórias, a variável log-normal descreve a multiplicação de variáveis aleatórias.
O exemplo mais conhecido de processo multiplicativo em ecologia é o modelo de crescimento populacional geométrico estocástico.
Neste modelo, o tamanho da população no tempo $$t+1$$ e o produto do tamanho da população no tempo anterior, $$t$$, multiplicado pela taxa de crescimento populacional $$R$$:
$$N_{t+1} \ = \ R cdot N_t$$
Se $$R$$ varia ao longo do tempo, podemos descrevê-la como uma variável aleatória. Portanto, o tamanho da população será o resultado da multiplicação de muitos realizações de uma variável aleatória. Neste cenário, as abundâncias de um conjunto de espécies com dinâmicas populacionais independentes seguirão uma distribuição log-normal.
Para simular esta situação, criamos uma função que reitera a equação de crescimento de uma população time vezes, e repete este procedimento para N populações de tamanho inicial N0, sendo o valor de $$R$$ uma variável uniforme, com valores entre Rmin e Rmax:
pops <- function(N,N0,Rmin,Rmax,time){
results <- matrix(nrow=N,ncol=time)
results[,1] <- N0
for(i in 1:N){
for(z in 2:time){
results[i,z] <- results[i,z-1]*runif(1,Rmin,Rmax)
}
}
results
}
O resultado desta função é uma matriz com N linhas (espécies) e time colunas (os intervalos de tempo). Com ela, simulamos a dinâmica populacional de 200 espécies por 20 intervalos de tempo, com valor médio do $$R=1$$, e atribuímos o resultado a um objeto:
abunds <- pops(200,500,Rmin=0.8,Rmax=1.2,time=20)
Com isto podemos fazer o histograma de densidade das abundâncias das 200 espécies no último intervalo de tempo:
hist(abunds[,ncol(abunds)], prob=T)
E sobrepor a curva da função de densidade da log-normal, com os parâmetros estimados da amostra de 200 populações:
curve(dlnorm(x,meanlog=mean(log(abunds[,ncol(abunds)])),
sdlog=sd(log(abunds[,ncol(abunds)]))),
add=T, col="blue")
Se a log-normal é um bom modelo para descrever as abundâncias, seus logaritmos devem seguir uma distribuição normal. Podemos verificar isto visualmente com um gráfico de quantil:
qqnorm(log(abunds[,ncol(abunds)])) qqline(log(abunds[,ncol(abunds)]))
Recursos para Estudo
Resumo da Aula
Na Internet
- Portal sobre distribuições de probabilidades na Wikipedia: http://en.wikipedia.org/wiki/Probability_distribution
- Distribuições interativas on-line do Statistics Online Computational Resource da UCLA: http://www.socr.ucla.edu/htmls/SOCR_Distributions.html
- Capítulo sobre variáveis aleatórias do e-book de Probabilidade e Estatística da UCLA: http://wiki.stat.ucla.edu/socr/index.php/EBook#Chapter_IV:_Probability_Distributions
- Mapa interativo de relações entre as distribuições de probabilidades. Um resumo em html do execelente mapa de Leemis & McQueston (2008).
- Um excelente resumo das propriedades e relações entre distribuições de probabilidade:
- Leemis, L. M., and J. T. McQueston. 2008. Univariate Distribution Relationships. The American Statistician 62:45-53.pdf na página do autor
- Várias atividades em JAVA com a normal no livro on-line Seeing Statistics : http://www.seeingstatistics.com/seeing1999/normal/normal.html
- Life is log-normal : argumentação provocadora a favor do uso da log-normal ao invés da normal, com link para o artigo e uma demonstração animada.
Variáveis Aleatórias Contínuas mais Usadas
* UNIFORME
- Parâmetros: $$a,b$$
- Parâmetros no R:
min,max - Função no R:
[dpq]unif - Suporte: $$a, b$$
- Assimetria: não
- Esperança: $$\frac{a+b}{2}$$
- Variância: $$\frac{(b-a)^2}{12}$$
- Parâmetros: $$\lambda$$
- Parâmetros no R:
rate - Função no R:
[dpqr]exp - Suporte: $$0, \infty$$
- Assimetria: direita
- Esperança: $$frac{1}{\lambda}$$
- Variância: $$frac{1}{\lambda^2}$$
* GAMA
- Parâmetros: $$s,a$$ OU $$r,a$$
- Parâmetros no R:
scale,shapeOUrate,shape - Função no R:
[dpqr]gamma - Suporte: $$0, \infty$$
- Assimetria: direita
- Esperança: $$as \ = \ \frac{a}{r}$$
- Variância: $$as^2 \ = \ \frac{a}{r^2}$$
* WEIBULL
- Parâmetros: $$s,a$$
- Parâmetros no R:
scale,shape - Função no R:
[dpqr]weibull - Suporte: $$0, \infty$$
- Assimetria: direita a não
- Esperança: $$s\Gamma(1+\frac{1}{a})$$
- Variância: $$s^2\Gamma(1+\frac{2}{a})-\mu^2$$
* BETA
- Parâmetros: $$a,b$$
- Parâmetros no R:
shape1,shape2 - Função no R:
[dpqr]beta - Suporte: $$0, 1$$
- Assimetria: direita,esquerda,não
- Esperança: $$\frac{a}{a+b}$$
- Variância: $$\frac{ab}{(a+b)^2(a+b+1)}$$
* NORMAL
- Parâmetros: $$\mu,\sigma$$
- Parâmetros no R:
mean,sd - Função no R:
[dpqr]norm - Suporte: $$-\infty, \infty$$
- Assimetria: não
- Esperança: $$\mu$$
- Variância: $$\sigma^2$$
- Parâmetros: $$\mu,\sigma$$
- Parâmetros no R:
meanlog,sdlog - Função no R:
[dpqr]lnorm - Suporte: $$0, \infty$$
- Assimetria: direita
- Esperança: $$e^{\mu+\sigma^2/2}$$
- Variância: $$\(e^{\sigma^2}-1)e^{2\mu+\sigma^2}$$
Pesquisa
Indique os tutoriais e partes da leitura básica que merecem mais atenção na discussão aqui.